Das „umgekehrte Ertragswertverfahren“
Aufgrund der zuletzt stark gestiegenen Immobilienpreise wird die Aufteilung von Grundstückskaufpreisen in Grund und Boden sowie Gebäude immer wichtiger. Die Aufteilung ist wichtig, weil (lediglich) das Gebäude steuerlich abgeschrieben werden kann. Wenn nicht bereits im (notariellen) Kaufvertrag eine entsprechende Aufteilung vereinbart wurde, muss diese mit Hilfe einer Bewertungsmethode vorgenommen werden.
Sowohl aus theoretischer wie auch aus praktischer Sicht ist eine solche Aufteilung (ähnlich wie die Ermittlung von „Unternehmensbestandteilen“ als Teilwerte) schwierig wenn nicht unmöglich: Grund und Boden sowie Gebäude bilden eine ökonomische Einheit; die einzelnen Bestandteile können für sich nicht exisitieren bzw. Cashflows generieren.
Als (vermeintliche) Lösung dieses Problems wurde jüngst das sog. „umgekehrte Ertragswertverfahren“ vorgeschlagen. Da dieses Verfahren offenbar in der Beratungspraxis Anklang findet, stellen Markus Diller und ich in einem kurzen Aufsatz („Kaufpreisaufteilung bei Grundstücken: Neue Methoden, alte Probleme“, DStR 2023, 1638) dar, dass bei diesem Verfahren im besten Fall (d.h. bei konsistenter Herleitung des Verfahrens) letztlich nur „einmal im Kreis“ gerechnet wird. Hier werden die wichtigesten Eckpunkte wiedergegeben.
Das „reguläre“ Ertragswertverfahren
Beim Ertragswertverfahren ergibt sich der Wert eines Gebäudes als Summe der abgezinsten „Gebäudereinerträge“ (d.h. der auf das Gebäude entfallenden Cahsflows) über die Restnutzungsdauer, also: \[G=g \times RBF_{r,n}.\]
Der Wert des Grund und Bodens wird ensprechend als Summe der abgezinsten Bodenwertverzinsungsbeträge (also der auf den Boden entfallenden Cashflows) ermittelt; da die Nutzungsdauer des Grund und Bodens unendlich ist, handelt es sich dabei um eine ewige Rente: \[B=\frac{b}{r}.\]
Voraussetzungen und Grundidee
Wurde eine Immobilie erworben, ist in der Regel der Kaufpreis \( K \) bekannt. Das umgekehrte Ertragswertverfahren setzt voraus, dass der Wert des Grund und Bodens \( B \) als Produkt von Fläche und Bodenrichtwert ermittelt werden kann und also ebenfalls bekannt ist. Nun könnte der Wert des Gebäudes schlicht als Differenz \( G = K - B \) berechnet werden. Der Gebäudeanteil ergäbe sich damit als \[ \gamma = \frac{G}{K} = \frac{G}{G+B}. \] Diese sog. „Restwertmethode“ wird jedoch vom BFH regelmäßig nicht zugelassen.
Das umgekehrte Ertragswertverfahren geht deshalb einen Umweg: Statt den Wert des Gebäudes ins Verhältnis zum Kaufpreis zu setzen, werden die periodischen Größen Gebäudereinertrag und Bodenwertverzinsungsbetrag herangezogen.
Variablen
| \(K\) | Kaufpreis | |
| \(B\) | Bodenwert | |
| \(b\) | Bodenwertverzinsungsbetrag | |
| \(G\) | Gebäudewert | |
| \(g\) | Gebäudereinertrag | |
| \(r\) | Liegenschaftszins | |
| \(n\) | Gebäude(rest)nutzungsdauer | |
| \(RBF_{r,n}\) | \(\frac{(1+r)^n-1}{(1+r)^n\times r}\) | Rentenbarwertfaktor |
| \(\gamma\) | Gebäudeanteil | |
| \(B_1\) | \(B_1+B_2=B\) | Bodenwert Teil 1 |
| \(B_2\) | \(B_1+B_2=B\) | Bodenwert Teil 2 |
Grundform
Grundsätzlich wird beim umbekehrten Ertragswertverfahren der Gebäudereinertrag ins Verhältnis zur Summe aus Bodenwertverzinsungsbetrag und Gebäudereinertrag gesetzt: \[\gamma^{uE} = \frac{g}{g+b} = \frac{\frac{G}{RBF_{r,n}}}{\frac{G}{RBF_{r,n}} + r\times B} .\]
Wenn die Gebäuderestnutzungsdauer gegen unendlich geht (\(\lim_{n\rightarrow \infty} RBF_{r,n}=1/r\)) ergibt sich wieder die Aufteilung nach der Restwertmethode. Dies gilt auch dann, wenn die Restnutzungsdauer des Grund und Bodens begrenzt wird und sich (von oben) der Gebäuderestnutzungsdauer annähert.
Bei endlicher Gebäudenutzungsdauer und unendlicher Bodennutzungsdauer wird hier der Gebäudeanteil gegenüber der Restwertmethode überschätzt (\(RBF_{r,n}<1/r\)).
Die Verzerrung kommt daher, dass durch das Abstellen auf periodische Größen eine Information – nämlich die Nutzungsdauer – verloren geht. Die Gebäude-Cashflows sind aufgrund der geringeren Nutzungsdauer relativ größer als die unendlichen Boden-Cashflows.
Begrenzung des Bodenwerts auf die Gebäude-Nutzungsdauer
Um diese Verzerrung auszugleichen, wird für die Gebäudeanteilsberechnung nur der Teil der Bodenwertverzinsungsbeträge berücksichtigt, der auf die Gebäuderestnutzungsdauer entfällt. Der entsprechende „Bodenwert Teil 1“ ergibt sich als \[ B_1 = b \times RBF_{r,n}\] (vgl. Abbildung).
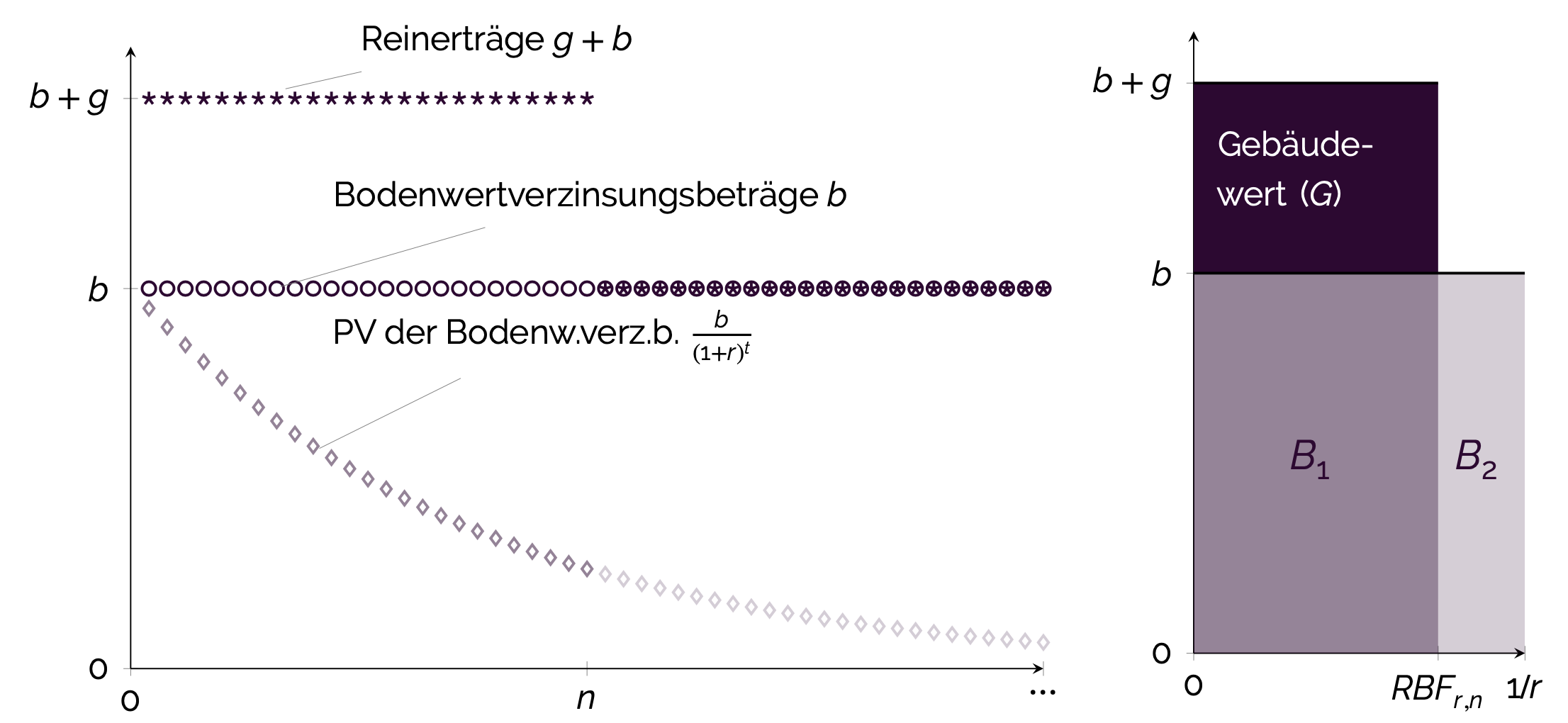
Fazit
Das umgekehrte Ertragswertverfahren kann angewendet werden, wenn die unterschiedlichen Nutzungsdauern von Gebäude und Grund und Boden wie oben beschrieben berücksichtigt werden. Es wird dadurch aber nichts „gewonnen“: Man könnte schlicht vom (bekannten) Kaufpreis den (bekannten) Bodenwert abziehen, um den Gebeäudewert zu erhalten.
Unsystematische Herleitung in der bisherigen Literatur
Hier wird der Bodenwertverzinsungsbetrag \(b=r\times B\) ebenfalls „gedämpft“ (in rot dargestellter Faktor). Der Bodenwertverzinsungsbetrag ist jedoch konstant; er ändert sich (jedenfalls in diesem Modellrahmen) nicht im Zeitablauf. Im Ergebnis bewertet dieses Verfahren den Gebäudeanteil systematisch zu hoch (der in rot dargestellte Faktor ist immer kleiner als 1).